Fuente:
Planeamiento y Control de Operaciones / Principios y Técnicas (resumen)
Carlos Romero Shollande
11. Modelos de Pronósticos
- Modelos cuantitativos
Requieren de datos históricos de tipo numérico, obtenidos mediante técnicas adecuadas de recopilación, para ser luego procesados mediante procedimientos mecánicos que producen resultados cuantitativos.
Las técnicas cualitativas suelen usarse para modificar pronósticos generados mediante métodos cuantitativos.
- Modelos cualitativos
Cuando hay pocos o se carece de datos históricos, las empresas confían en la experiencia y el buen juicio administrativo para generar predicciones del futuro.
12. Modelos Cuantitativos - Empíricos
Los modelos empíricos son modelos sencillos que suponen que los periodos recientes son los mejores pronosticadores del futuro.
12.1. Modelo Empírico Simple
En este modelo el pronóstico de la demanda para el siguiente periodo es igual a la demanda observada en el periodo actual.
- Modelos cualitativos
Cuando hay pocos o se carece de datos históricos, las empresas confían en la experiencia y el buen juicio administrativo para generar predicciones del futuro.
12. Modelos Cuantitativos - Empíricos
Los modelos empíricos son modelos sencillos que suponen que los periodos recientes son los mejores pronosticadores del futuro.
12.1. Modelo Empírico Simple
En este modelo el pronóstico de la demanda para el siguiente periodo es igual a la demanda observada en el periodo actual.
Yt+1’ = Yt
Donde:
Yt = Demanda real del periodo t
Yt+1’ = Demanda pronosticada para periodo siguiente a t
Gráfica 12. Resultados del modelo empírico simple
Gráfica 12. Resultados del modelo empírico simple
12.2. Modelo Empírico con Tendencia
En este modelo de pronóstico se debe tomar en cuenta una tendencia de la demanda.
El incremento (o decremento) observado en la demanda en los dos últimos periodos se usa para ajustar la demanda actual con miras a elaborar un pronóstico.
Donde:
Yt-1 = Demanda real del periodo anterior a t
Gráfica 13. Resultados del modelo empírico con tendencia
12.3. Modelo Empírico Estacional
Se aplica patrones estacionales. Por ejemplo, la demanda de un determinado mes del año anterior puede servir para pronosticar el mes correspondiente del año actual. Así mismo, los pronósticos de demanda para cada uno de los meses del año entrante será un simple reflejo de la demanda real observada en esos mismos meses durante el año pasado.
Donde:
m = número de periodos del patrón estacional (12 meses, 6 bimestres o 4 trimestre al año)
Gráfica 14. Resultados del modelo empírico estacional
12.4. Modelo Empírico Estacional con Tendencia
Pueden combinarse la tendencia con la estacionalidad para pronosticar la demanda del siguiente periodo, usando la siguiente expresión:
Gráfica 15. Resultados del modelo empírico estacional con tendencia
12.5. Modelo Empírico con Proporción de Cambio
En este modelo se pronostica la demanda utilizando una proporción de cambio.
Gráfica 16. Resultados del modelo empírico con proporción de cambio
13. Modelos con Promedios
Los modelos de promedios se desarrollan con base en un promedio de observaciones ponderadas.
Todos estos modelos se utilizan para pronosticar la demanda futura para un corto plazo
13.1. Modelo de Promedio Simple
Se obtiene encontrando el promedio simple de todos los valores pertinentes y usando después este promedio para pronosticar el siguiente periodo.
13.1. Modelo de Promedio Simple
Se obtiene encontrando el promedio simple de todos los valores pertinentes y usando después este promedio para pronosticar el siguiente periodo.
Donde:
n = número de periodos históricos
Gráfica 17. Resultados del modelo de promedio simple
Gráfica 17. Resultados del modelo de promedio simple
13.2. Modelo del Promedio Móvil Simple
Se obtiene encontrando la media de un conjunto específico de valores (observaciones recientes) y empleándolo después para pronosticar el siguiente periodo.
Donde:
Mt = promedio móvil en el periodo t
m = # de periodos para obtener cada promedio móvil
Gráfica 18. Resultados del modelo del promedio móvil simple
Gráfica 18. Resultados del modelo del promedio móvil simple
Luego se calcula el segundo promedio móvil (Mt’).
Se calcula un valor similar a la intersección de una línea con la ordenada (at):
A continuación se calcula un factor, similar a la medición de una pendiente (bt) que cambia a través de la serie:
Se determina el pronóstico para el periodo p en el futuro:
Donde:
p = número de periodos a pronosticar hacia el futuro
m = número de periodos para el promedio móvil
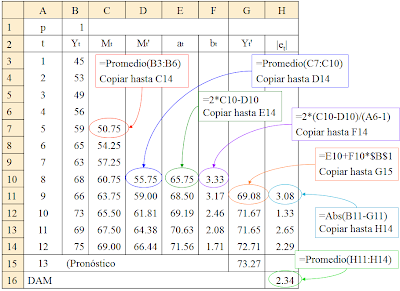
Gráfica 19. Resultados del modelo del promedio móvil doble
13.4. Modelo del Promedio Móvil Ponderado
Cada una de las demandas históricas que intervienen en el promedio puede tener su propia ponderación. El resultado de la suma de las ponderaciones es 1.0.
a1 + a2 + ……...+ am = 1
El pronóstico para el siguiente periodo es:
El pronóstico para el siguiente periodo es:
Donde:
a1, a2, .., an : Coeficientes de ponderación del periodo i
Gráfica 20. Resultados del modelo de promedio móvil ponderado
14. Modelos Atenuación Exponencial
Los modelos de atenuación se basan en promedios de valores anteriores de una serie en forma decreciente (exponencial). Las observaciones se ponderan, asignando mayor peso a las más recientes.
14.1. Modelo Atenuación Exponencial Simple
El pronóstico para el periodo t+1 es:
Donde:
a = Constante de atenuación (0 < a < 1)
Para interpretar mejor a la ecuación anterior:
Y t+1’ = aYt + Yt’ - aYt’
Y t+1’ = Yt’ + a (Yt - Yt’)
El nuevo pronóstico es el pronóstico anterior (Yt’) más a veces el error (Yt – Yt’) del pronóstico anterior.
El primer valor del pronóstico (Y1’) debe ser igual al primer valor real (Y1).
Otro enfoque para inicializar Yt’ consiste en promediar las primeras m observaciones.
La clave del análisis es el valor de a.
Si desea que el pronóstico sea estable y atenúe las variaciones aleatorias, entonces a debe ser pequeño.
Si desea respuesta rápida al cambio real en el patrón, entonces a debe ser grande.
Para estimar a se utiliza un procedimiento iterativo en Excel, que minimiza el (EMC).
Se calculan los pronósticos para a igual a 0.1, 0.2, …., 0.9, y para cada uno se calcula el EMC. Para generar pronósticos futuros, se elige el valor de a que produce el EMC más pequeño.
Gráfica 21. Resultados del modelo de atenuación exponencial simple
Gráfica 21. Resultados del modelo de atenuación exponencial simple
14.2. Modelo Atenuación Exponencial Doble
También se le conoce como Modelo de Brown.
Se utiliza para pronosticar series de tiempo que tienen una tendencia lineal.
Primero, se calcula el valor simple atenuado exponencialmente usando la siguiente ecuación:
Donde:
At = Valor del promedio atenuado exponencialmente de Yt en el periodo t
a = Constante de atenuación (0 < a < 1)
Luego, se calcula el valor doblemente atenuado exponencialmente:
Calcular el factor adicional de ajuste, similar a la medición de la intersección de la ordenada con una recta que cambia durante la serie de tiempo:
Calcular el factor adicional de ajuste, similar a la medición de la pendiente de una recta que cambia durante la serie de tiempo.
Por último, se formula el pronóstico para p periodos en el futuro.
Si no hay datos disponibles, el primer valor del promedio atenuado exponencial (A1) debe ser igual al primer valor real (Y1) y el primer valor doblemente atenuado exponencial (A1’) también debe ser igual al primer valor real (Y1).
Si existen datos históricos, el primer valor del promedio atenuado exponencial y el primer valor doblemente atenuado exponencial deben ser iguales al promedio de dichos datos
Gráfica 22. Resultados del modelo de atenuación exponencial simple
Gráfica 22. Resultados del modelo de atenuación exponencial simple
14.4. Modelo de Holt
Es un modelo que emplea dos parámetros: la atenuación exponencial y la tendencia.
El procedimiento, en primer lugar, consiste en atenuar exponencialmente el promedio de la serie de tiempo.
Luego se realiza la estimación de la tendencia:
Finalmente se calcula el pronóstico para p periodos en el futuro:
En donde:
Tt = tendencia del periodo t
p = número de periodos a pronosticar al futuro
a = constante de atenuación del promedio de los datos (0 £ a £ 1)
b = constante de atenuación de estimación de tendencia (0 £ b £ 1)
El primer valor del promedio atenuado exponencial (A1) se establece en forma similar que en el modelo de Brown.
El primer valor del promedio atenuado exponencial (A1) se establece en forma similar que en el modelo de Brown.
Si no hay datos disponibles, el primer valor atenuado de la estimación de la tendencia (T1) debe ser cero (0).
Si existen datos, el valor inicial de la tendencia se estima por la pendiente de la ecuación obtenida de dichos datos.
Gráfica 23. Resultados del modelo de Holt
Gráfica 23. Resultados del modelo de Holt
14.5. Modelo de Winter
Es un modelo que emplea tres parámetros: la atenuación exponencial, la tendencia y la estacionalidad.
El procedimiento, en primer lugar, consiste en atenuar exponencialmente el promedio de la serie de tiempo.
Enseguida se realiza la estimación de la tendencia:
Luego se hace la estimación de la estacionalidad:
Donde:
a = Constante de atenuación del promedio de los datos (0 <= a <= 1)
b = Constante de atenuación de la estimación de tendencia (0 <= b <= 1)
g = Constante de atenuación de la estacionalidad (0 <= g <= 1)
At = Valor atenuado en el periodo t
Tt = Estimación de la tendencia del periodo t
St = Estimación de la estacionalidad del periodo t
L = Longitud de la estacionalidad
p = Número de periodos a pronosticar en el futuro
Finalmente se calcula el pronóstico para p periodos en el futuro:
Finalmente se calcula el pronóstico para p periodos en el futuro:
El primer valor del promedio atenuado exponencialmente (A1) y el primer valor atenuado de la estimación de la tendencia (T1) se deben establecer de igual forma que en el Modelo de Holt.
Si no existen datos, los valores estimados de la estacionalidad de los L-1 periodos anteriores se establecerán en uno (1).
Si existen datos, se descompone la serie de tiempo.
A los L primeros pronósticos se asigna primer valor real
Gráfica 24. Resultados del modelo de Winter
Gráfica 24. Resultados del modelo de Winter





































No hay comentarios:
Publicar un comentario