Fuente:
Planeamiento y Control de Operaciones / Principios y Técnicas (resumen)
Carlos Romero Shollande
6. Sistemas de Inventarios
• Modelo de Inventario para un Sólo Periodo
– Decidir una compra en un periodo dado (Ejemplo: vendedor de camisetas para un partido de fútbol)
– Buscar el balance de los costos de inventario por exceso o desabastecimiento de existencias
• Modelos de Inventarios para Varios Periodos
– Modelos de la Cantidad Fija de la Orden
• Activados por los eventos (Ejemplo: funcionando fuera de existencias)
– Modelos para Periodos Fijos de Tiempo
• Activados por el tiempo (Ejemplo: Venta mensual pedida por venta representativa)
6.1. Modelo de Inventario para un solo Periodo
Este tipo de modelo se debe seguir para incrementar el tamaño del inventario tan grande como la probabilidad de vender la última unidad agregada.
Donde
Co = Costo por unidad de demanda sobrestimada
Cu = Costo por unidad de demanda subestimada
P = Probabilidad de que la unidad sea vendida
Ejemplo 3 (Modelo de un Sólo Periodo)
Nuestro equipo de basketball de la Escuela esta jugando en un torneo deportivo este fin de semana. Basado en nuestra experiencia pasada vendimos un promedio de 2,400 polos con una desviación estándar de 350. Obtuvimos $10 por cada polo que vendimos en el partido, pero perdimos $5 por cada polo que no se vendió. ¿Cuántos polos se debe fabricar para el partido?
Cu = $10
Co = $5
P ≤ $10 / ($10 + $5) = 0.667
Z.667 = 0.432.
Usar DISTR.NORM.STAND.INV(.667).
Nuestra necesidad: 2,400 + .432(350) = 2,551 polos
6.2. Modelo de Inventario para Varios Periodos
6.2.1. Modelo de la Cantidad Fija de la Orden
Supuestos:
• La demanda del producto es constante y uniforme a lo largo del periodo
• El tiempo de entrega (desde la colocación de la orden hasta su recepción) es constante
• El precio por unidad del producto es constante
• El costo de mantener el inventario esta basado en un inventario promedio
• Los costos por colocar la orden o la preparación son constantes
• Todas las demandas del producto deberán ser satisfechas (no se permiten ordenes atrasadas)
Notación del Modelo de la Cantidad Fija de la Orden (EOQ)
ED = Existencias disponibles
t = Tiempo en meses
Q = Cantidad económica de pedido o lote de compra
tQ = Tiempo en que se consume el lote económico de compra
s = Existencias de seguridad o de reserva
ts = Tiempo que protege el inventario de protección
EM = Inventario máximo cuando llega un nuevo pedido
NR = Cantidad en almacén al momento de hacer un pedido (punto de reorden o nivel de reposición)
e = Tiempo de entrega de suministro en meses (interno más el del proveedor), debe ser constante
D = Demanda anual
x = Número de pedidos al año (frecuencia)
Cuadro 14. Modelo de la Cantidad Fija de la Orden (EOQ)
La demanda mensual (DM) de un artículo es de 300 unidades/mes, el lote de compra establecido es de 900 unidades y el inventario de seguridad es de 500 unidades.
Así mismo, se tiene que el tiempo de espera interno de suministro es de 0.2 meses y el tiempo de espera por el proveedor es de 1.8 meses
a)¿Cuál es el número de pedidos anuales realizado?
b)¿Cuál es el nivel de reposición o punto de pedido?
c)¿Por cuánto tiempo de retraso en la entrega por el proveedor protege el inventario de seguridad?
a)¿Cuál es el número de pedidos anuales realizado?
b)¿Cuál es el nivel de reposición o punto de pedido?
c)¿Por cuánto tiempo de retraso en la entrega por el proveedor protege el inventario de seguridad?
Solución
a) Número de pedidos al año
a) Número de pedidos al año
c) Tiempo de protección del inventario de seguridad
Costos del Inventario
• Costos de preparación de órdenes
Costos por preparar una orden cada vez que se coloca una orden de reabastecimiento
• Costos por mantener el inventario
Costos de almacenaje, manejo, seguro, daños, depreciación, de oportunidad de capital, etc
• Costos de preparación (o cambio de producción)
Costos para preparar el equipo en forma específica para un determinado producto, etc
• Costos por desabastecimiento
Costos cuando las existencias de un artículo se agotan o cuando una orden se cancela, etc
Costo de la Orden de Compra (CO)
- Costo de funcionamiento del Dpto. de Compras
- Costo de Recepción
- Gastos postales, fax, Internet, etc
- Gastos de Contabilidad
donde:
A = Costo adquisición de un pedido (constante)
x = Frecuencia o número de pedidos al año
Costo por Mantener Inventario (CM)
- Pérdidas del interés de los capitales inmovilizados
- Pérdidas del interés de los capitales inmovilizados
- Costo de Oportunidad de Capital
donde:
u = Precio unitario del artículo (constante)
I = Tasa del costo por mantener inventario (en tanto por ciento al año del precio de factura)
H = Costo de mantenimiento de inventario por unidad por año (esta basado en un inventario promedio)
Tasa del Costo por Mantener Inventario (I)
donde:
ib = Interés de los bancos
ip = Interés de recursos propios
ir = interés del riesgo y dejar de invertir en otros negocios
Pb = % de inversión proveniente de financiamiento de los bancos
Pp = % de inversión con recursos propios
Pb = % de inversión proveniente de financiamiento de los bancos
Pp = % de inversión con recursos propios
Ejemplo 5 (Sistema ABC)
Cuadro 15. Datos del problema:
A | B | |
1 | Precio de factura del artículo (u) $: | 5 |
2 | Cantidad anual requerida del artículo (D): | 100 |
3 | Costo de adquisición (A) ($ / pedido | 8 |
4 | Costo de posesión (% precio factura) (I) | 15 |
Se pide:
• Determinar los costos combinados de adquisición y posesión para 1 a 10 pedidos
• ¿Cuál es el lote de compra más económico?
• Efectuar la solución gráfica, considerando:
- Eje X: cantidad por lote
- Eje Y: costos
Solución
Solución
Cuadro 16. Cálculos para el sistema ABC.
Cuadro 17. Solución gráfica.
Meta de la Minimización de Costos
Al reunir los costos del artículo, de mantenimiento y de la orden, se determina la curva del costo total, la cual es usada para determinar el punto de la orden de inventario Qopt que minimice el costo total
Cuadro 18. Minimización del costo total.

Cuadro 19. Fórmula del Modelo Básico de la Cantidad Fija de la Orden (EOQ)
CT = Costo total anual
D = Demanda anual
u = Costo / unidad
Q = Cantidad de la Orden
A = Costo de colocar una orden
I = Costo anual de mantenimiento y almacenaje / unidad de inventario
Derivando la EOQ
Derivando la EOQ
Se calcula la primera derivada de la función del costo total con respecto a Q, luego la derivada se iguala a cero (minimización del costo), obteniéndose el lote económico de compra Qopt .
También se necesita un punto de reorden que avise que se debe colocar una orden
Punto de reorden:
đ = Demanda diaria promedio (constante)
e = Tiempo de entrega (constante)
Siempre e > 0
Ejemplo 6
Dada la información siguiente, ¿cuál es la cantidad fija de la orden (EOQ) y el punto de reorden?
Demanda Anual = 1,000 unidadesEjemplo 6
Dada la información siguiente, ¿cuál es la cantidad fija de la orden (EOQ) y el punto de reorden?
Días por año (para la demanda diaria promedio = 365
Costo por colocar una orden = $10
Costo de mantenimiento por unidad por año = $2.50
Tiempo de entrega = 7 días
Costo por unidad = $15
Solución
Punto de reorden:
En resumen, usted puede poner una orden óptima con 90 unidades.
Cuando usted tiene un nivel en curso de 20 unidades, para satisfacer la demanda oportunamente, debe usted poner el pedido siguiente de 90 unidades.
6.2.2. Modelo de los Periodos Fijos de Tiempo
Notación del Modelo de Periodos Fijos de Tiempo
ED = Existencias disponibles
t = Tiempo en meses
X = Número de pedidos al año óptimo (frecuencia óptima)
tX = Tiempo en el que se consume el lote de compra
q = Cantidad pedida o lote de compra
s = Existencias de seguridad o de reserva
ts = Tiempo que protege el stock de protección
EM = Stock máximo cuando llega un nuevo pedido
NR = Cantidad en almacén al momento de hacer un pedido (punto de reorden o nivel de reposición)
e = Tiempo de entrega o de espera de suministro en meses (interno más el del proveedor)
D = Demanda anual
Cuadro 20. Modelo de Periodos Fijos de Tiempo
Ejemplo 7
Con los datos del problema (2) determinar la frecuencia económica de compra y efectuar la solución gráfica.
Frecuencia económica: En la tabla de la solución del problema (2) se observa: X = 7 pedidos / año
Cuadro 21. Solución gráfica.
Costo de la Orden de Compra (CO)
Como:
Luego: CO = X.A (lineal)
donde:
A = Costo adquisición de un pedido o colocar una orden
X = Frecuencia o número de pedidos al año óptimo
Costo por Mantener Inventario (CM)
Como:
Luego: (Hipérbola equilátera)
donde:
u = Precio unitario del artículo (precio de factura)
I = Tasa del costo por mantener inventario (en tanto por ciento al año del precio de factura)
Cuadro 22. Fórmula del Modelo Básico de Periodos Fijos de Tiempo
CT = Costo total anual
D = Demanda anual
u = Costo / unidad
X = Frecuencia óptima
A = Costo de colocar una orden
I = Costo anual de mantenimiento y almacenaje / unidad de inventario
Derivando la Ecuación
Se calcula la primera derivada de la función del costo total con respecto a X, luego la derivada se iguala a cero (minimización del costo), obteniéndose la frecuencia económica de pedido Xopt .
Ejemplo 8
La demanda anual de un producto es 800 unidades, el costo por colocar una orden es de $10, la tasa del costo por mantener inventario por unidad por año es de 10% y el costo por unidad es de $15. ¿Cuál es la frecuencia económica?
Solución:

























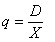
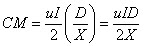



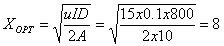
No hay comentarios:
Publicar un comentario